Jeff Tupper’s quine
Math Python NumPy Quine
Yesterday, a friend sent me Numberphile’s video, “The ‘Everything’ Formula”
The video describes a neat formula that acts as a plotter for any arbitrary bitmap of size 106x17. For some reason, it is often referred to as “Tupper’s self-referential formula”:
$$\frac{1}{2} < \left\lfloor \mathrm{mod}\left(\left\lfloor \frac{y}{17} \right\rfloor 2^{-17 \lfloor x \rfloor - \mathrm{mod}\left(\lfloor y\rfloor, 17\right)},2\right)\right\rfloor$$
Jeff Tupper’s original paper indeed contains this formula (Figure 13), but it is listed only as an example of two-dimensional graphing and it is never described as self-referential. While it is a cool mind-scratcher, it is definitely not self-referential, but a quine. It can produce itself in a different modality, but only when looked at the right place on the infinite x-y plane. I like Arvind Narayanan’s comparison with the infinite monkey theorem. Can a monkey hitting keys at random for an infinite amount of time eventually type Shakespeare’s Hamlet? Yes, almost surely. The question is where can we find it in the monkey’s infinite string. Can a function that describes every possible 106x17 (1802!) bitmap somewhere on x-y plane contain some representation of the original function? Sure can, but we need to know where exactly.
There are dozens of articles and blog posts that go in details of how does it work and some even propose an actual self-referential formula. The posts I have linked explain the theory behind the formula, and much better than I can. Instead, on this quiet Easter Monday I want to demonstrate how I have implemented both finding where can we find the bitmap we are looking for, as well as plotting this bitmap, all in modern Python.
Plotting the formula
Let’s start with the plotting. The image that we are looking for should be at 0 < x < 106 and k < y < k + 17. In the original paper, k is defined as
960 939 379 918 958 884 971 672 962 127 852 754 715 004 339 660 129 306 651 505 519 271 702 802 395 266 424 689 642 842 174 350 718 121 267 153 782 770 623 355 993 237 280 874 144 307 891 325 963 941 337 723 487 857 735 749 823 926 629 715 517 173 716 995 165 232 890 538 221 612 403 238 855 866 184 013 235 585 136 048 828 693 337 902 491 454 229 288 667 081 096 184 496 091 705 183 454 067 827 731 551 705 405 381 627 380 967 602 565 625 016 981 482 083 418 783 163 849 115 590 225 610 003 652 351 370 343 874 461 848 378 737 238 198 224 849 863 465 033 159 410 054 974 700 593 138 339 226 497 249 461 751 545 728 366 702 369 745 461 014 655 997 933 798 537 483 143 786 841 806 593 422 227 898 388 722 980 000 748 404 719
A straight forward way to plot this is to evaluate the function for each x,y point at this separately. Instead, we can vectorize computations with NumPy and use Pillow for loading and saving images:
import numpy as np
from PIL import Image
K = ... # omitted for readability
# build a meshgrid for X coordinates from 0 to 106 and Y coordinates from K to K+17
x, y = np.meshgrid(range(106), range(K, K+17))
# evaluate Tupper's formula for all points at once
result = 0.5 < ((y // 17) // (2 ** (17 * x + y % 17))) % 2
# in my implementation we need to mirror the image due to coordinates mismatch
result = np.fliplr(result)
# convert into an image and save to disk
Image.fromarray(result).save('original.png')
Here’s the “self-replicating” result: 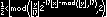
We have confirmed that the approach works, now let’s see how we can find more interesting bitmaps!
Finding k for arbitrary images
The algorithm is quite simple:
- Convert the 106x17 image of interest into a thresholded binary image where each pixel has value 0 or 1.
- Flatten the image column-wise into a single binary number that consists of 106*17=1802 ones or zeros.
- Convert this number into base-10 and multiply by 17.
Let’s translate this into code. Again, we’ll use NumPy and PIL.
import numpy as np
from PIL import Image
# load the image and convert it to a numpy array
image = np.array(Image.open(path_to_image))
# threshold the image: convert the array to binary and then back to int
image = image.astype(bool).astype(int)
# transpose (image must be encoded column-wise), mirror (to match original coordinates frame) and flatten
image = np.fliplr(image.T).flatten()
# represent array as one integer in base 10 and multiply it by 17
K = int(''.join(map(str, image)), 2) * 17
# for readability let's split the found number by 3 characters
from textwrap import wrap
print(f'Found K: {" ".join(wrap(str(K), 3))}')
Let’s see if this will work for the OG: 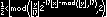
Found K: 960 939 379 918 958 884 971 672 962 127 852 754 715 004 339 660 129 306 651 505 519 271 702 802 395 266 424 689 642 842 174 350 718 121 267 153 782 770 623 355 993 237 280 874 144 307 891 325 963 941 337 723 487 857 735 749 823 926 629 715 517 173 716 995 165 232 890 538 221 612 403 238 855 866 184 013 235 585 136 048 828 693 337 902 491 454 229 288 667 081 096 184 496 091 705 183 454 067 827 731 551 705 405 381 627 380 967 602 565 625 016 981 482 083 418 783 163 849 115 590 225 610 003 652 351 370 343 874 461 848 378 737 238 198 224 849 863 465 033 159 410 054 974 700 593 138 339 226 497 249 461 751 545 728 366 702 369 745 461 014 655 997 933 798 537 483 143 786 841 806 593 422 227 898 388 722 980 000 748 404 719
That’s exactly the same string as above, yay! Time to find find some interesting k’s.
Other k
As a tribute to the author, let’s find k of Jeff Tupper’s name: 
Found K: 385 815 185 034 138 158 985 870 922 709 187 771 741 984 863 903 001 560 903 755 944 700 527 424 584 051 315 029 117 989 906 439 493 180 632 249 939 860 962 369 068 130 333 226 454 308 011 056 898 770 189 860 026 183 100 209 457 279 325 986 175 729 482 270 868 521 087 312 425 053 904 627 001 175 969 513 613 540 074 140 325 118 540 773 528 302 948 665 290 791 255 891 024 244 612 978 717 349 953 081 144 003 722 839 141 078 743 527 892 814 519 951 422 463 077 169 240 686 548 347 390 436 099 422 493 685 020 088 219 659 235 193 486 350 953 092 824 772 778 233 932 879 750 089 176 444 321 163 669 351 665 248 816 840 127 309 058 081 171 960 635 932 943 715 857 693 920 045 698 334 277 341 544 448
Mustering all my artistic skill, I managed to draw something easily recognizable even on such a small image: 
Found K: 126 142 104 213 220 484 299 803 993 442 062 205 409 077 505 220 633 202 015 858 972 307 182 501 421 645 782 823 217 849 945 196 989 219 566 869 642 586 856 002 258 241 479 301 667 237 018 424 945 404 030 790 228 025 510 765 380 030 265 144 252 981 546 142 589 226 719 086 965 652 739 520 845 129 864 851 583 864 577 815 519 135 290 434 195 548 911 229 646 938 854 682 829 338 643 067 177 226 847 816 952 758 734 166 379 981 459 848 756 683 277 095 647 000 957 329 360 499 307 384 746 219 787 041 087 624 524 570 154 355 080 970 812 831 032 393 680 420 031 478 481 534 582 784
We can go futher and add support for RGB(A) images by grayscaling and thresholding before converting image to a number, allowing us to find k of some fun things.
if image.ndim == 3:
# thresholding value was chosen experimentally ¯\_(ツ)_/¯
image = image[..., :3].mean(-1) > (image.mean() / 1.5)
For example, we can try to find k of a cat who is being yelled at by a woman: 
Found K: 851 030 412 628 336 556 165 809 369 962 109 912 804 161 242 368 430 933 212 288 014 494 536 807 542 740 734 381 671 364 065 155 879 388 013 869 494 956 962 061 134 763 310 263 193 385 575 072 149 137 089 604 705 201 819 322 847 554 746 397 401 554 468 442 840 234 615 665 452 154 695 967 266 451 351 629 936 505 011 951 742 325 309 194 431 147 721 355 712 298 208 733 534 626 570 288 417 823 332 710 025 407 637 465 753 296 616 837 452 115 490 622 693 556 930 112 201 054 318 590 446 660 494 224 496 302 101 506 150 764 129 717 619 346 698 940 226 775 371 940 997 279 460 630 181 000 578 484 533 391 638 594 731 484 579 785 972 285 338 008 247 656 925 936 746 496
Result:
Or a surprised pikachu: 
Found K: 100 471 937 400 773 042 105 488 795 487 079 558 956 078 370 881 471 858 986 932 192 035 983 663 503 559 690 104 085 241 627 816 344 060 029 535 358 169 730 565 614 348 280 274 258 391 956 093 706 487 773 600 207 321 552 633 572 512 727 519 083 578 975 536 089 240 998 241 402 260 568 596 955 034 368 758 047 736 965 380 237 422 807 289 192 867 659 494 212 761 961 844 085 991 026 277 158 315 733 803 429 051 940 595 481 874 380 651 187 292 245 665 209 511 827 991 598 028 036 167 858 029 884 225 988 105 814 239 390 403 337 695 473 230 329 464 921 830 026 338 051 548 823 510 917 702 632 449 767 686 964 811 819 836 113 753 470 019 547 288 874 741 950 634 085 738 923 194 014 636 840 792 896 8
Result:
All in all, that was a fun one day project!
– Ilja